ADONIS | Buckingham Lab

Description

It has been called the “deep abyss” and even the “big blue”. Though many have ventured into its depth, only a fraction of its expanse is known to man.

However, a revolutionary underwater electronic imaging technique currently under development by a dozen Scripps Institution of Oceanography (SIO) scientists is promising to shed new light into the ocean’s murkiest depths.

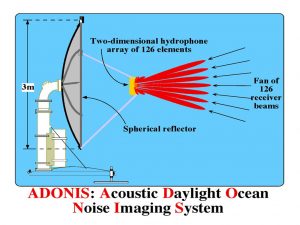
The technique, known as the Acoustic Daylight Ocean Noise Imaging System (ADONIS), uses the ambient noise present in the ocean- created by everything from passing ships, breaking waves and popping of bubbles- to create images of objects in the water.

Objects in the ocean modify the noise fields around themselves in the ways directly tied to their shape, composition and position.

Dr Michael J. Buckingham, an SIO professor of ocean acoustics and an ADONIS co-developer, came upon the idea for acoustic daylight in 1985 while working on sonar for the English Ministry of Defense.

There are two basic ways of viewing underwater. They are using passive or active sonars. The active means that one can transmit a ‘ping’ and listen for an echo. In passive one listens for the sound produced by sources that are passing by, such as submarines, breaking waves, etc. Ambient noise in the ocean is equivalent to ambient light in the atmosphere. Given that background, it is assumed that there is a fair chance of using the ambient noise in the ocean to take photographs.

The Technology

ADONIS scientists compare acoustic daylight’s fundamental principles to that of photography- a camera, without a flash, uses ambient light reflected off an object to create an image of that object.

In Acoustic daylight imaging scientists use sound as their enabling medium. The ambient noise in the ocean serves as an analog of daylight field in the atmosphere.

ADONIS consists of a dish which is able to focus on slight variations in the ocean’s ambient noise field. With its three meters in diameter, it is capable of detecting high frequency sounds, between 8 and 80 kilohertz. The dish itself does not record the sound; it simply reflects the collected acoustics back to a series of 126 hydrophones- or underwater microphones- mounted on the front of the dish, facing inward. In turn, the hydrophones convert the acoustic image into a set of electrical signals, which, through a set of manipulations are rendered onto a Macintosh computer screen into real-time, false-color, pixilated images, which are refreshed 30 times per second.

As is the case with any scientific breakthrough, however, it takes a certain amount of time before the results can be fully appreciated by the public at large. The image itself is of rather poor quality; it is not the quality of a camera image. The reason for this is that the wavelength of light is very small, and across the human pupil there are something like 20000 wavelengths. The wavelengths used by ADONIS are a lot larger, and there is only about 300 wavelengths across the dish.. Therefore the aperture of the dish is quite small compared to the eye. In fact, achieving a similar resolution with sound would require a more-or-less unfeasible dish, measuring some 600 meters in diameter.

Nevertheless we all find encouragement in the results of our team’s testing so far. We compare the current state of acoustic daylight imaging to the developmental years of television. One day, television pioneers got an image on a screen, and it was not a very good quality image, but that was not important. The point was that there was an image.

Wet Runs

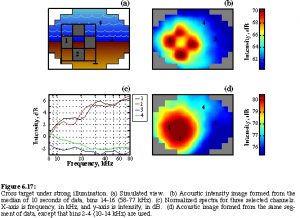
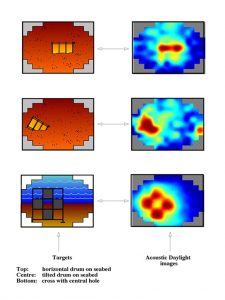
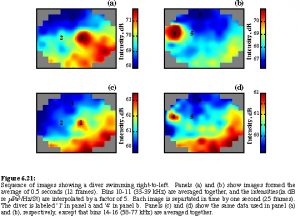
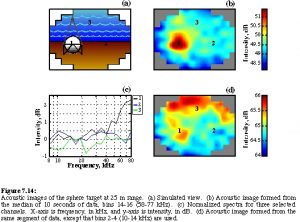
In August 1994, using one of SIO’s research platforms located off the coast of Point Loma, project scientists dropped the 3000-pound ADONIS into the ocean for the first time. Although scientist first tested acoustic daylight principles in the water off of Scripps Pier in mid-1991, the new acoustic lens, ADONIS, wasn’t constructed until the following year. In the 1994 test, ADONIS, scientists set up a target frame- containing one-meter-by-one-meter square panels which could be set up in various tic-tac-toe-like arrangements- on the ocean floor and tested ADONIS at various ranges from the target. Despite some initial setbacks concerning the flooding of the unit’s electrical circuitry, scientists were able to collect a good amount of raw data in which the shapes formed by the panels were visible on the computer screen. But more importantly, the images rendered on the screen confirmed that the acoustic daylight imaging was indeed feasible.

During the same initial test, scientists also erected the target frame at a distance of 40 meters from ADONIS, which, currently has a range of 80 meters and can resolve images which are one meter or larger in size.

ADONIS scientists conducted another test run of the system of the cost of Point Loma in December 1995, and although the results have not yet been released, they are encouraging. This data, contained on 70 CD-ROMs, is expected to be released within the next several months.

The ADONIS technology, once perfected, could serve a myriad of uses. The U.S. Navy, for example, could potentially use acoustic daylight imaging to detect the presence of mines in the ocean- some of which can be triggered by sonar- without causing them to explode. In addition, project scientists envision acoustic daylight technology being someday used to secure harbors from underwater attack, to monitor oil rigs and to perform counts of underwater marine-mammal populations. Acoustic daylight imaging could also be used by unmanned, underwater vehicles. A navigation system equipped with ambient noise imaging would allow these vehicles to steer themselves around underwater objects without human intervention.

People have been using acoustics to get information about the ocean for quite a while. The future of acoustic daylight is fairly good because more and more people and industries are interested in finding out what’s going on in the ocean. The best way of finding out is to use sound.

Data